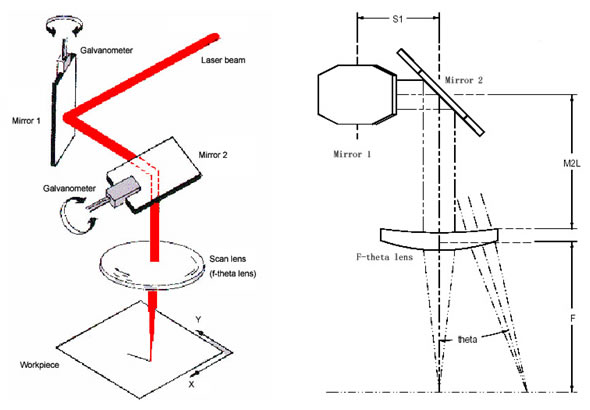
Basics of 2-axis Laser Scanners
A laser beam is reflected from two scan mirrors in turn, and directed through a focusing lens. The mirrors are capable of high speed deflection about a rotation axis, being driven by a galvo-scanner motor. In most cases the maximum deflection angle of the mirror is ±12.5° (often ±10° is a safer limit) either side of the non-deflected incidence angle of 45°.
Note that, for best performance, the lens will appear to be ‘the wrong way round’ when compared with a standard meniscus lens used in conventional focusing of a laser beam.
Some of the design objectives in specification of 2-axis laser scanners are:
-
Achievement of desired scanned field size
-
Maximization of scan speeds
-
Minimizing focused spot sizes
-
Lowest cost solutions
Some of the limitations to be considered are:
-
Quality factor Q (Q = M2) of the laser beam
-
Scan angle limitations
-
Loss of power due to beam-clipping
-
Physical aperture of the scanner head
Field of scan
The laser beam will be scanned over an angle q, equal to twice the mirror deflection angle. So, the typical scanned field might be q=±20° in both X and Y directions. (q=±25° would be the usual maximum scanned field). The field size is then approximately 2Ftanq in both X and Y.
The approximation arises because:
1) it is usually desirable to have a deliberate distortion characteristic in the scanner lens design so that the field position is proportional to q, not tanq.
2) scanning in two axes produces a geometrical distortion which is unrelated to the lens properties.
Focused spot size
The lower limit on spot size ‘d’ (1/e2 intensity diameter) for a laser beam of diameter ‘D’ (1/e2) is:
d = 13.5QF/D mm
Example: A TEM00 beam (Q=1) of 13.5mm (1/e2) diameter, focused by a perfect lens of 100mm focal length, will form a focused spot of 100mm diameter. (Taking a more realistic value of Q=1.5, the spot size would be 150mm).
Beam clipping and optical aberrations can lead to focused spot sizes which are larger than the minimum diffraction limited value found from the equation above.
Large field sizes demand the use of lenses of long focal length. In turn, this leads to increased focused spot size unless the beam diameter, mirror sizes, and lens diameter are all increased.
Spot sizes are given in the form of an average spot size over the whole, maximum, field-of-scan. A second figure, the standard deviation from average spot size, gives a measure of variation of the spot size to be expected over the field.
Beam clipping
The physical aperture of a laser scanner is often limited by a circular aperture of the scanner head, of diameter ‘A’ mm, say.
Beam clipping can occur at a circular aperture, even for a well-centred beam, when the ‘tails’ of the beam energy distribution is blocked by the metalwork. The percentage power loss at a circular aperture, for a TEM00 beam (Q=1) is shown in the following table:
Table: Power Loss
|
A/D |
0.8 |
1 |
1.2 |
1.4 |
1.6 |
1.8 |
2 |
|
Loss % |
27.8 |
13.5 |
5.6 |
1.98 |
0.6 |
0.15 |
0.03 |
The table indicates that, where the physical aperture of the scanner is limited to A mm diameter, the laser beam diameter D (1/e2) must be selected by a compromise between reduced spot size and power loss due to beam clipping. A value of D = A/1.4 would probably be acceptable for most laser scanner systems. Power loss due to beam clipping increases for de-centred beams.
Mirror design
Mirror (1) (or called Scan Mirror X)
The width of mirror (1) is determined by the beam diameter. It is easier to discuss this in terms of a ‘full beam diameter’ DF, where the definition of full diameter is, to some extent, arbitrary.
For example, a system designer might define DF as the measured diameter of a beam print in perspex [plexiglass]. Alternatively, DF may be the measured 99% power points, or perhaps a value chosen in the range 1.4D to 1.6D.
The mirror width W1 is slightly larger than the selected value of DF, sufficient to allow for minor misalignment. The length of mirror (1) is determined by the maximum angle of incidence imax on the mirror. Let a= (90°-imax). Then the mirror length is L1, where L1 = W1/sina. The large shape ‘chamfers’ on scanner mirrors are determined by the separation, S1, between mirrors (1) and (2); the scan angles, and the need that the mirrors should not collide during scanning.
Mirror (2) (or called Scan Mirror Y)
The width of mirror (2), W2, should be identical to the length of mirror (1). The length, L2, of mirror (2) is found from projection of the beam onto the second mirror at a distance of S1, and at maximum scan angle q. These mirrors are built and coated specifically for use with CO2 or YAG lasers. They have a very high laser damage threshold, measured at 1000W/mm of 1/e2 beam diameter (D).
F-theta characteristic
Lenses described as being ‘F-theta’, or ‘Fq’, type are designed so as to produce an off-axis spot at a location proportional to the scan angle. In turn, this may be directly proportional to a voltage applied to the galvo scanner motor. (A lens with zero distortion would form a spot at a field location of Ftanq). No 2-axis galvo scanner can have a true F-theta characteristic, due to distortion from use of two mirrors. Single-element lenses are designed to be the best compromise between smallest spot size and F-theta characteristic. Errors in F-theta characteristic are usually 2% - 3% for these single element lenses. Multi-element lenses allow design freedom enabling a closer approach to F-theta performance. Fq errors <0.36% are typical for this range, with only the 75mm FL type having a slightly greater value.
Lens design
All scanning lens designs are based on factors described above. For typical small scanner systems, limited to perhaps 10mm or 15mm full beam diameter, lenses of 48mm diameter have been found to be suitable. For 15mm beams, this lens size is only possible by minimizing the distances S1 and M2L. Each class of lens is designed for use with a specific range of beam diameters, and, more importantly, for a specific set of values S1 and M2L.
In each case the lens is designed to provide the best compromise performance for flat field, spot size and F-theta characteristic for the specified beam diameter and mirror locations, while avoiding beam-clipping at the lens mount.
For certain (longer focal length, single-element) lenses it is possible to obtain an improvement in performance by increasing the distance M2L. This necessitates the design/use of lenses of larger diameter (to avoid beam clipping).
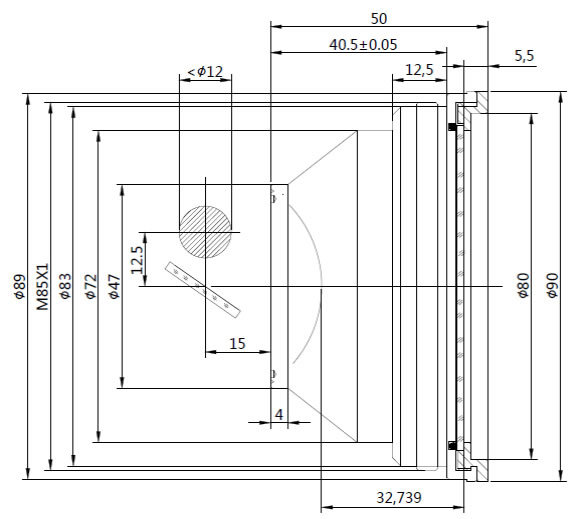
Typical parameters of marking head LSLC-1064-10-DIGI
Our marking head LSLC-1064-10-DIGI is designed for fiber laser 1064nm, 10mm entrance use. The designed distance L2 (m1) between the distance of 2 scan mirrors is 13.5mm and the distance L1(m2) between mirror Y and the top surface of the f-theta lens is 25.9mm.
Typical parameters of f-theta lens STY-1064-110-160
Laser wavelength: 1064nm
M1: 12.5mm
M2: 15mm
Max. beam entrance: 12mm
Max. angle: +/-28 degree
2Y: 156.4mm (110x110mm)
EFL: 160mm
BFL: 186.8mm
FFL: 190.8mm
WD: 181.2mm
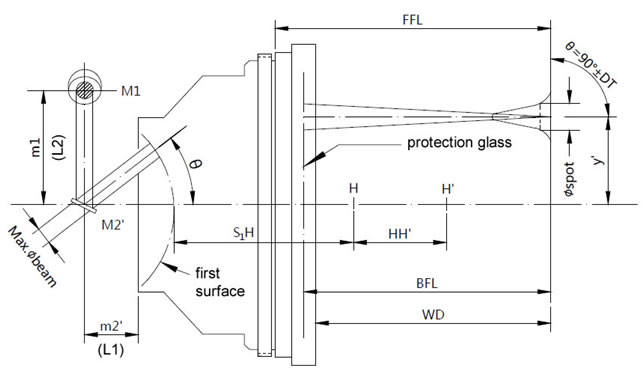
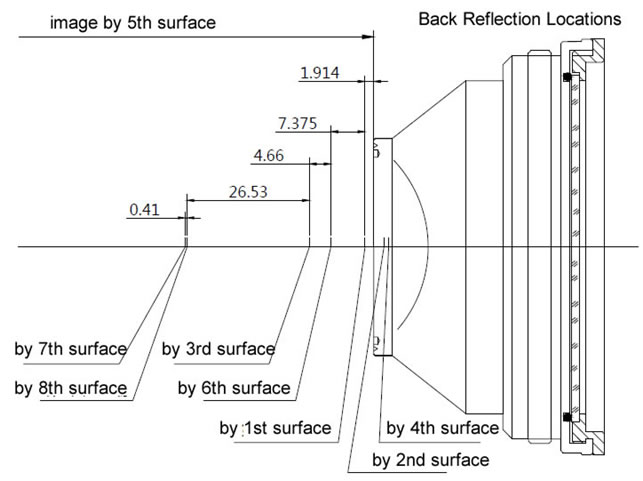
For laser marking applications, M1 and M2 may not be exactly same as the designed parameters. The allowed tolerance may be around 6-10mm, which does not result in obvious changes of marking performance.
The focused beam diameter is mainly decided by f-theta and laser beam quality.
 English
English Français
Français Deutsch
Deutsch euskara
euskara Русский язык
Русский язык Italiano
Italiano Português
Português Nederlands
Nederlands Polski
Polski Greek
Greek Lietuva
Lietuva Türkçe
Türkçe 日本語
日本語 한어
한어 中文
中文 தாமில்
தாமில் فارسی
فارسی हिंदी
हिंदी Tiếng Việt
Tiếng Việt ภาษาไทย
ภาษาไทย Pilipino
Pilipino Indonesia
Indonesia தாமில்
தாமில்





